除自身以外数组的乘积

题目

给你一个长度为 n 的整数数组 nums，其中 n > 1，返回输出数组 output ，其中 output[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积。

示例:

输入: [1,2,3,4] 输出: [24,12,8,6]

提示：题目数据保证数组之中任意元素的全部前缀元素和后缀（甚至是整个数组）的乘积都在 32 位整数范围内。

说明: 请不要使用除法，且在 O(n) 时间复杂度内完成此题。

进阶： 你可以在常数空间复杂度内完成这个题目吗？（ 出于对空间复杂度分析的目的，输出数组不被视为额外空间。）

来源：力扣（LeetCode） 链接：https://leetcode-cn.com/problems/product-of-array-except-self 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解决方法

方法一：左右乘积列表
思路

利用索引左侧所有数字的乘积和右侧所有数字的乘积相乘得到答案。

算法

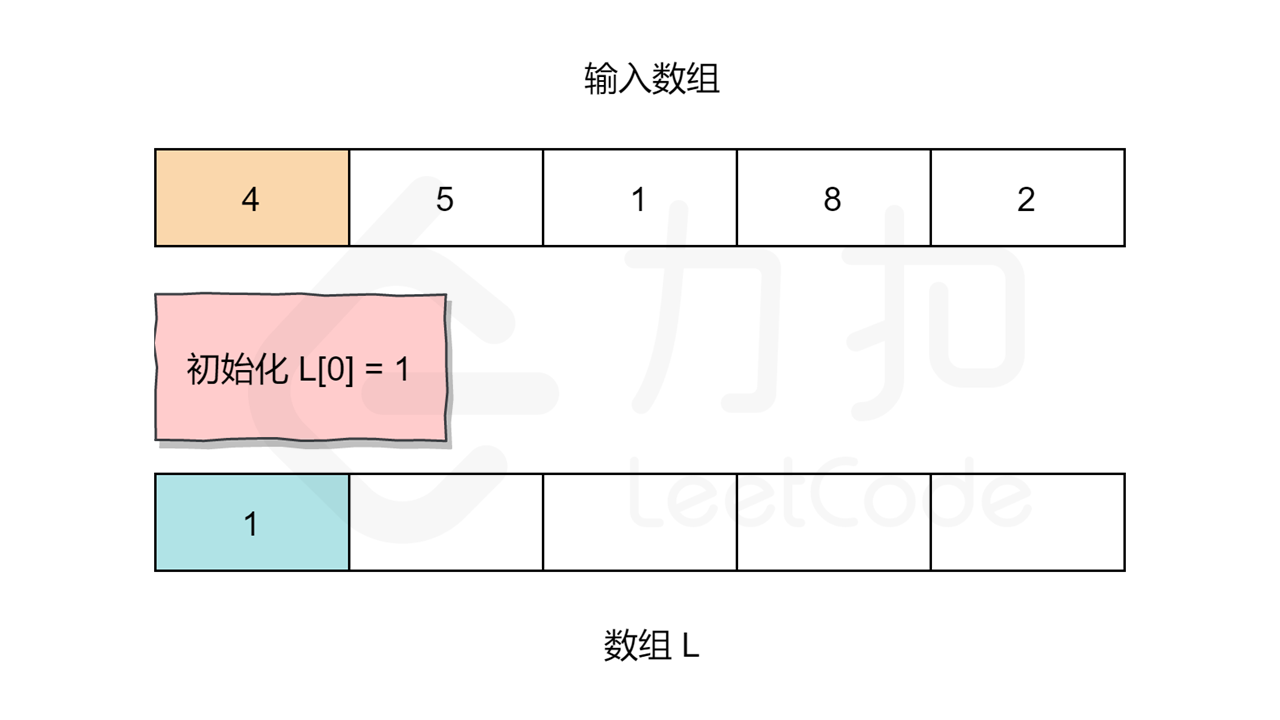
  1. 两个空数组 L 和 R 。对于给定的索引 i ，L[i] 代表的是 i 左侧所有的数字的乘积，R[i] 代表的是 i 右侧所有数字的乘积。

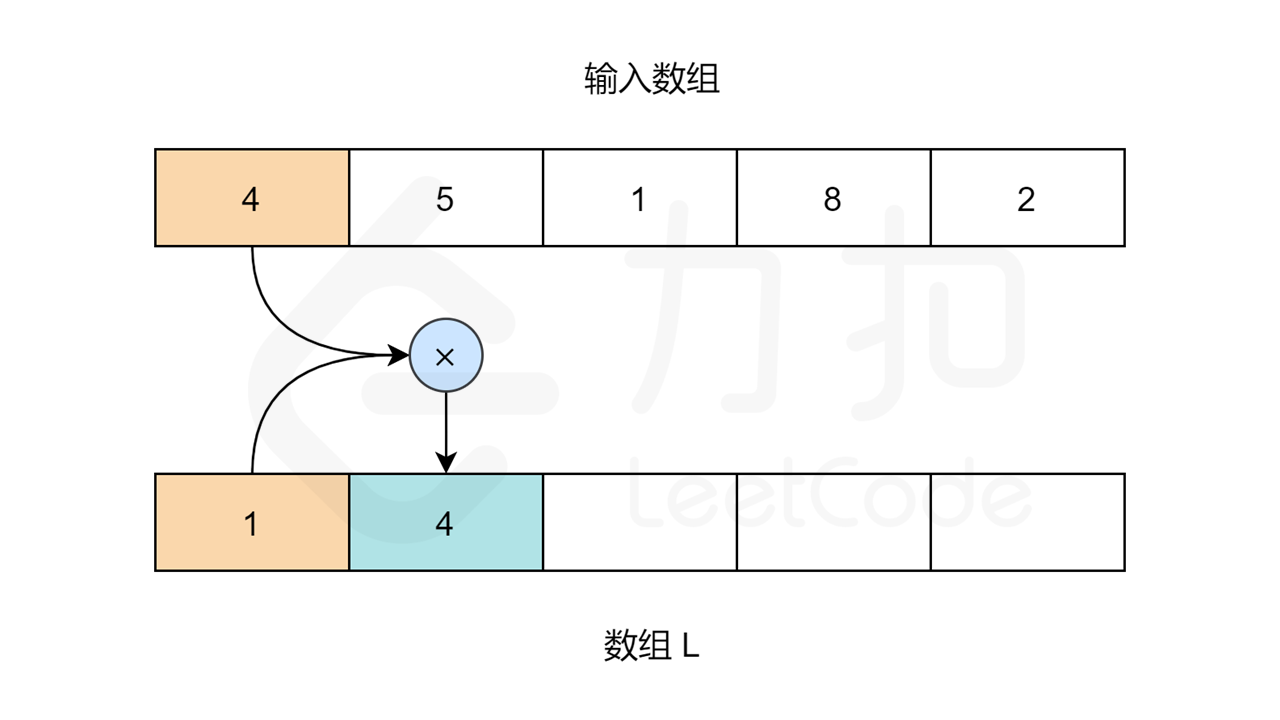
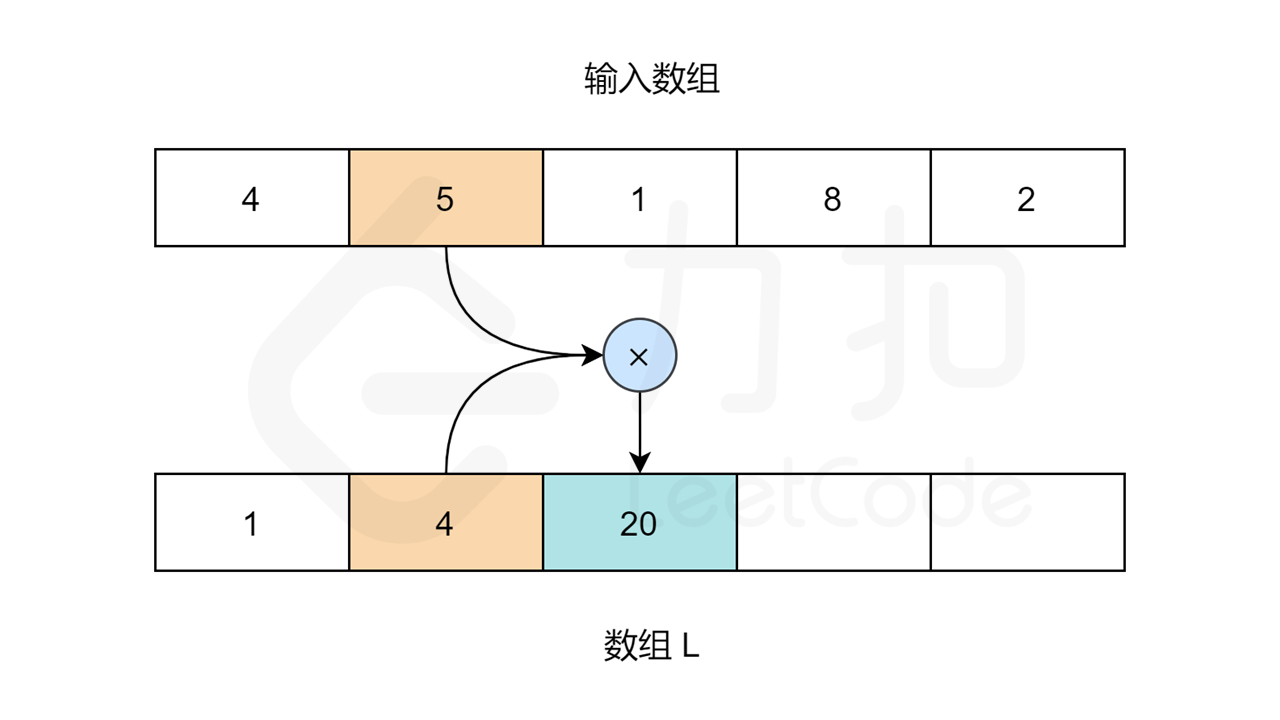
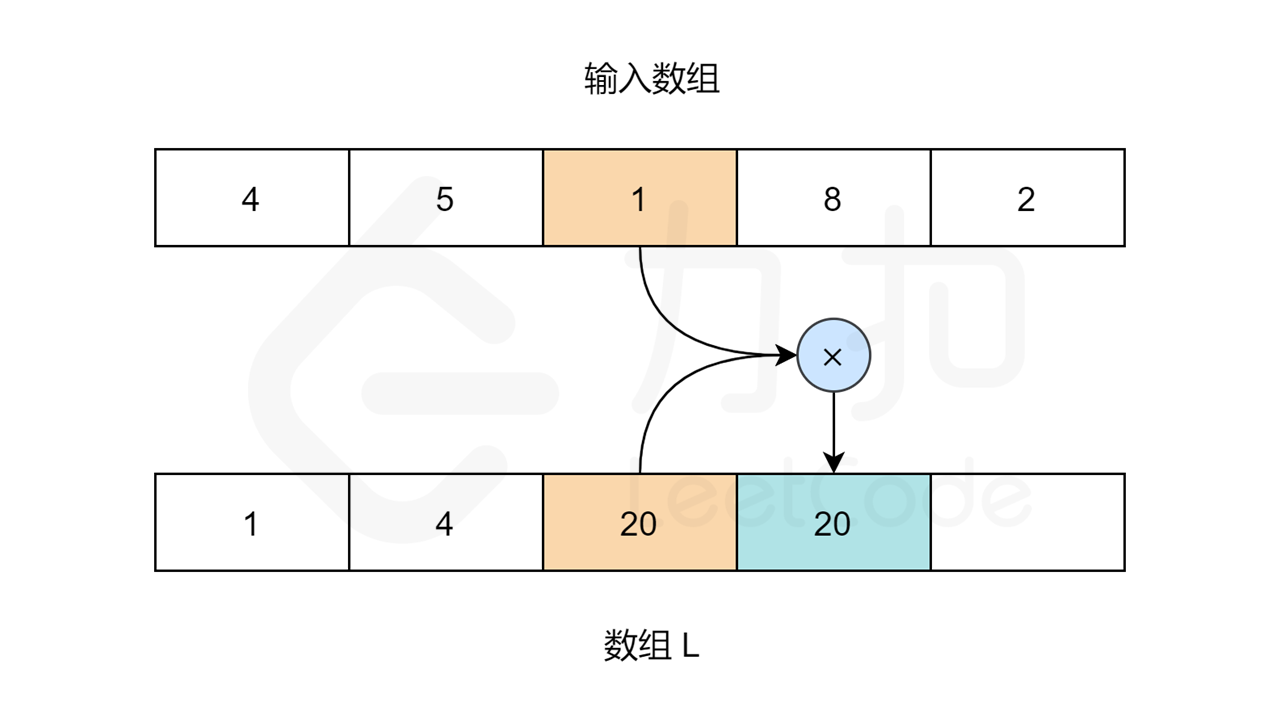
  2. 我们需要用两个循环来填充 L 和 R 数组的值。对于数组 L ，L[0] 应该是 1，因为第一个元素的左边没有元素。对于其他元素：L[i] = L[i-1] * nums[i-1] 。

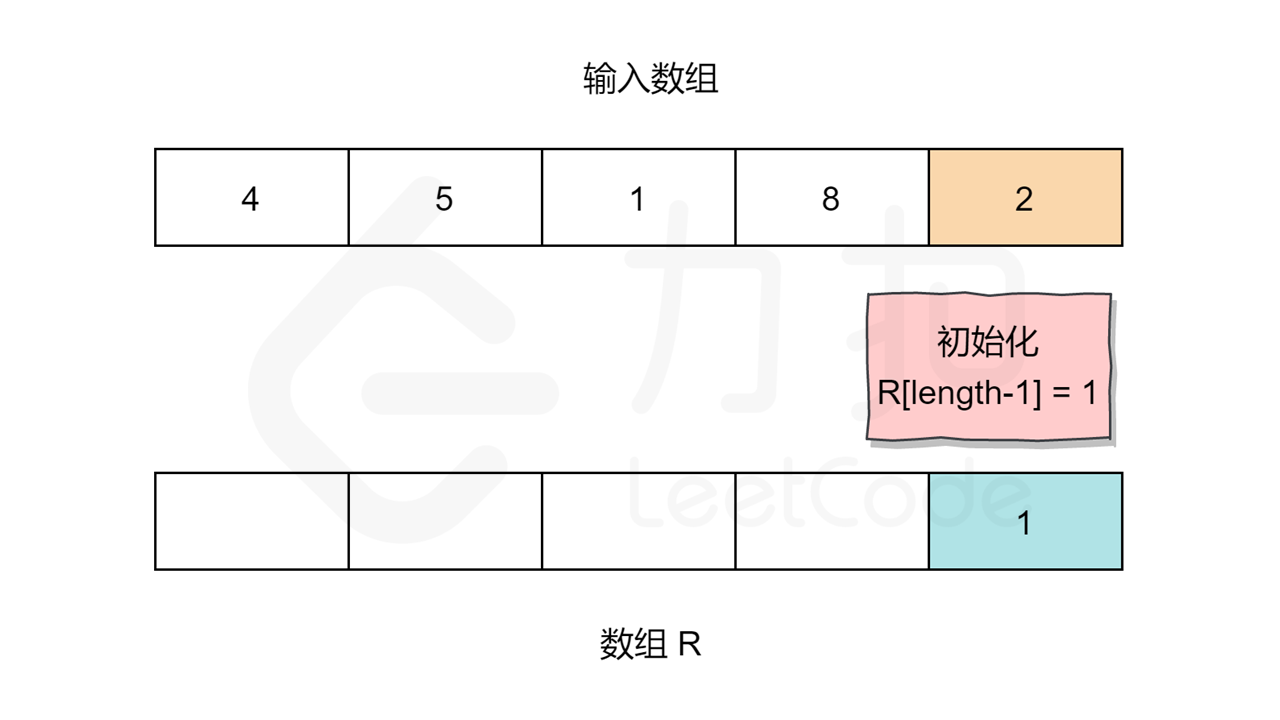
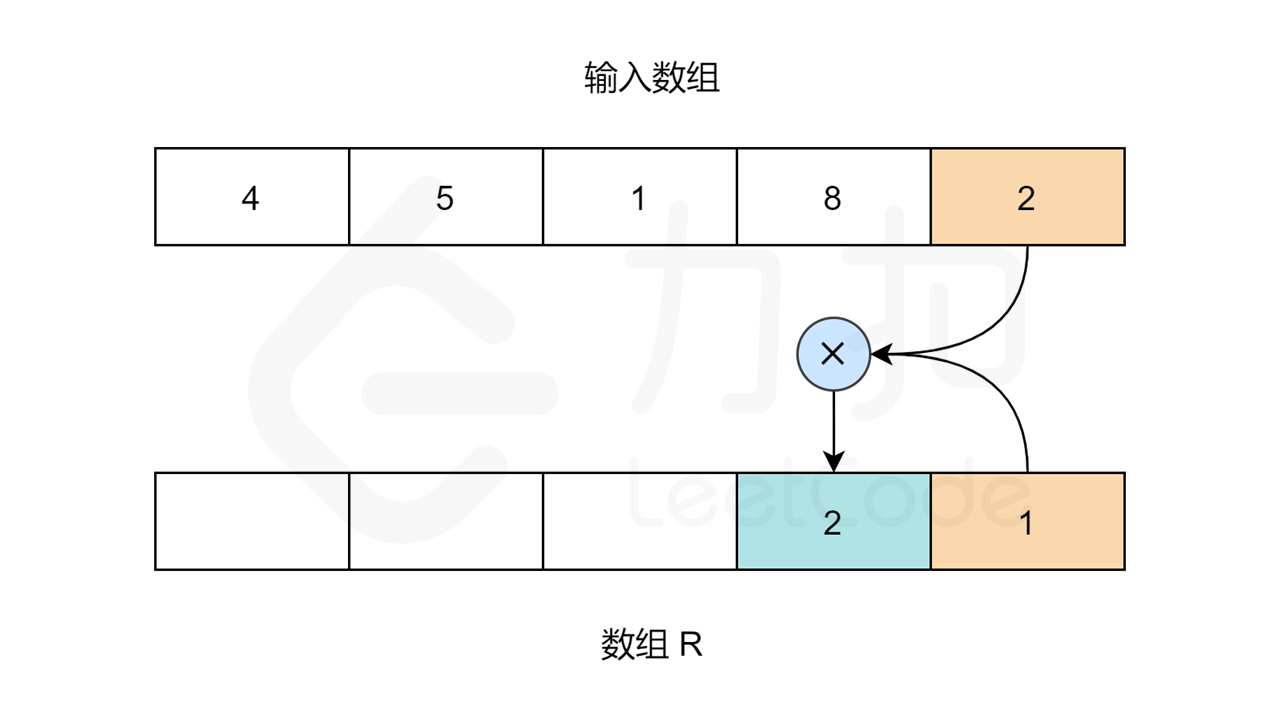
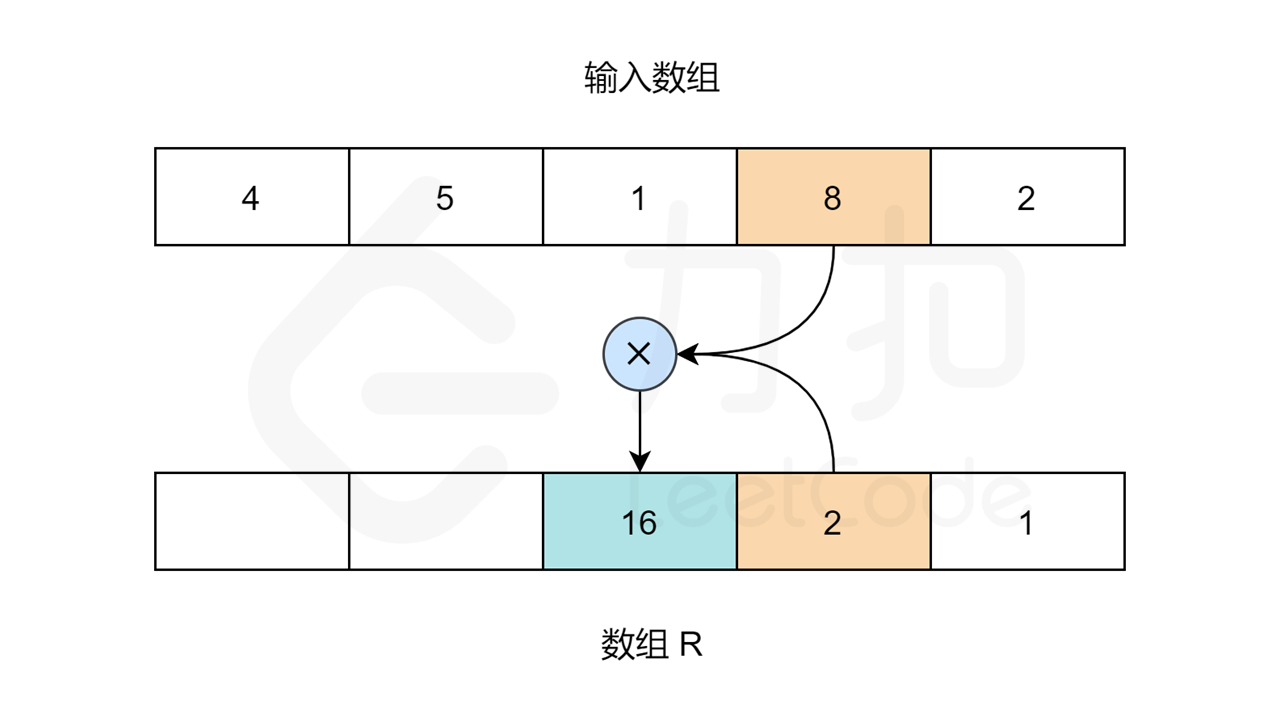
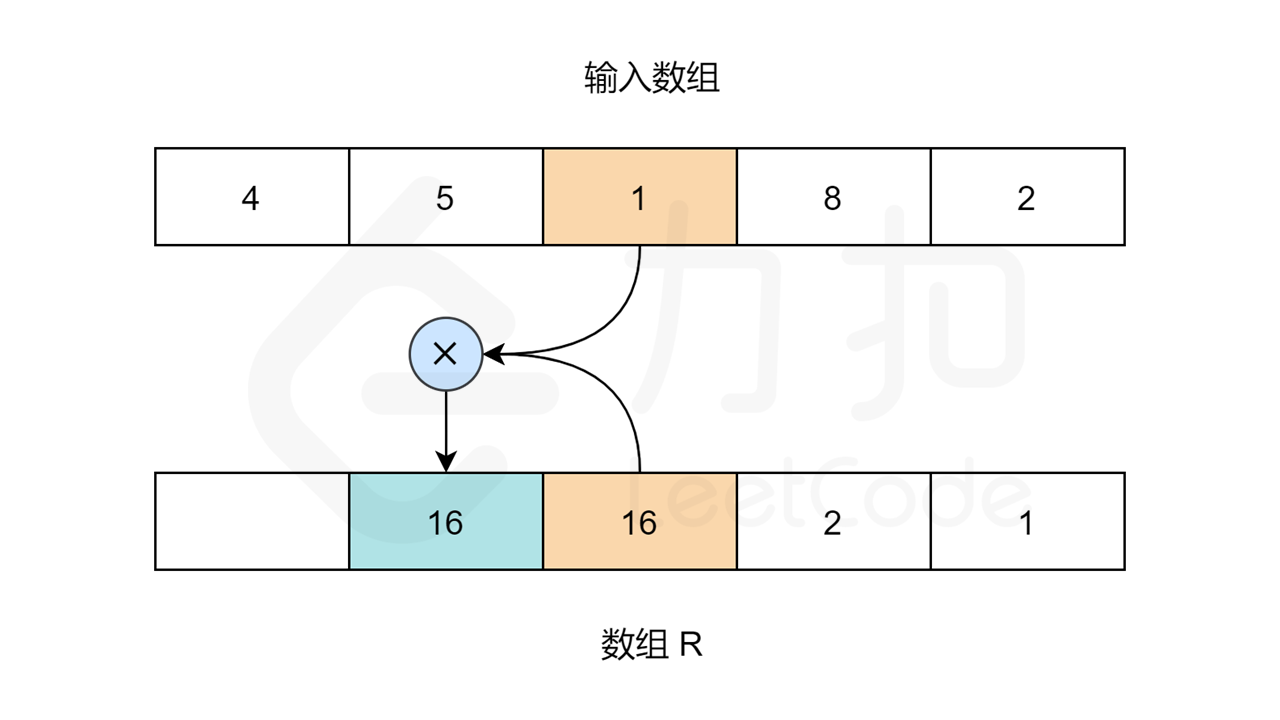
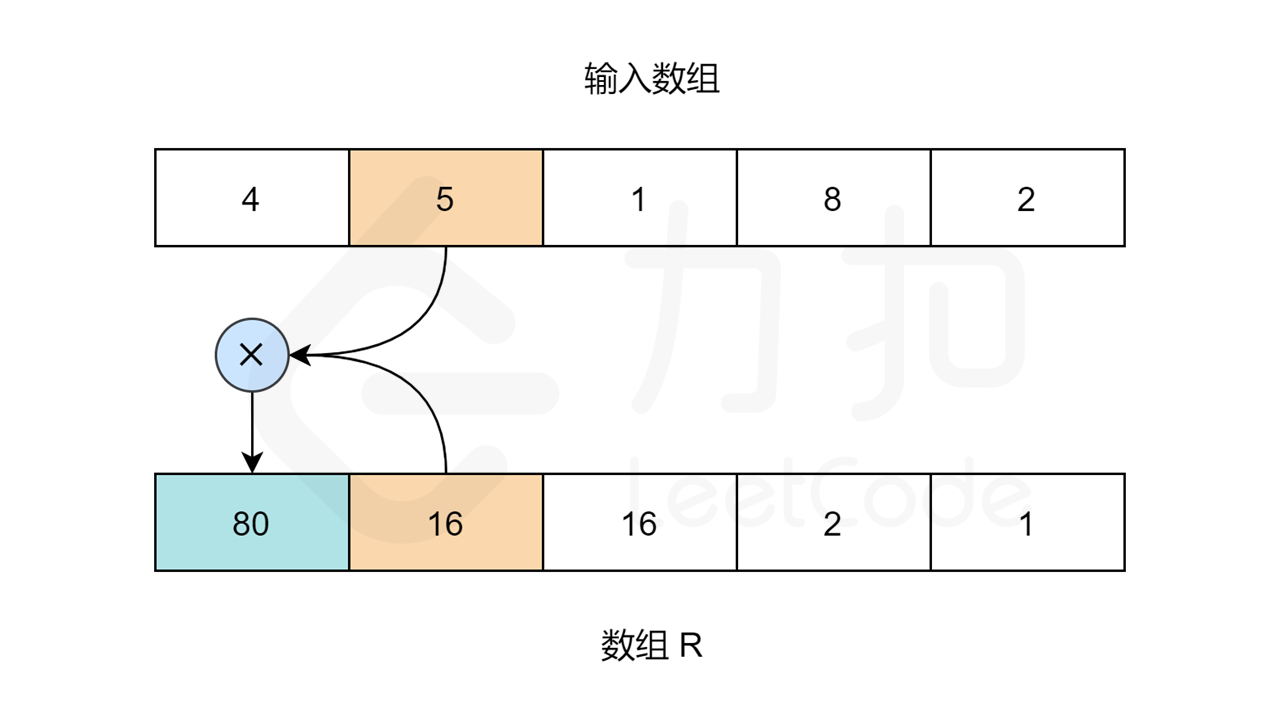
  3. 同理，对于数组 R ，R[length-1] 应为 1 。length 指的是输入数组的大小。其他元素：R[i] = R[i+1] * nums[i+1] 。

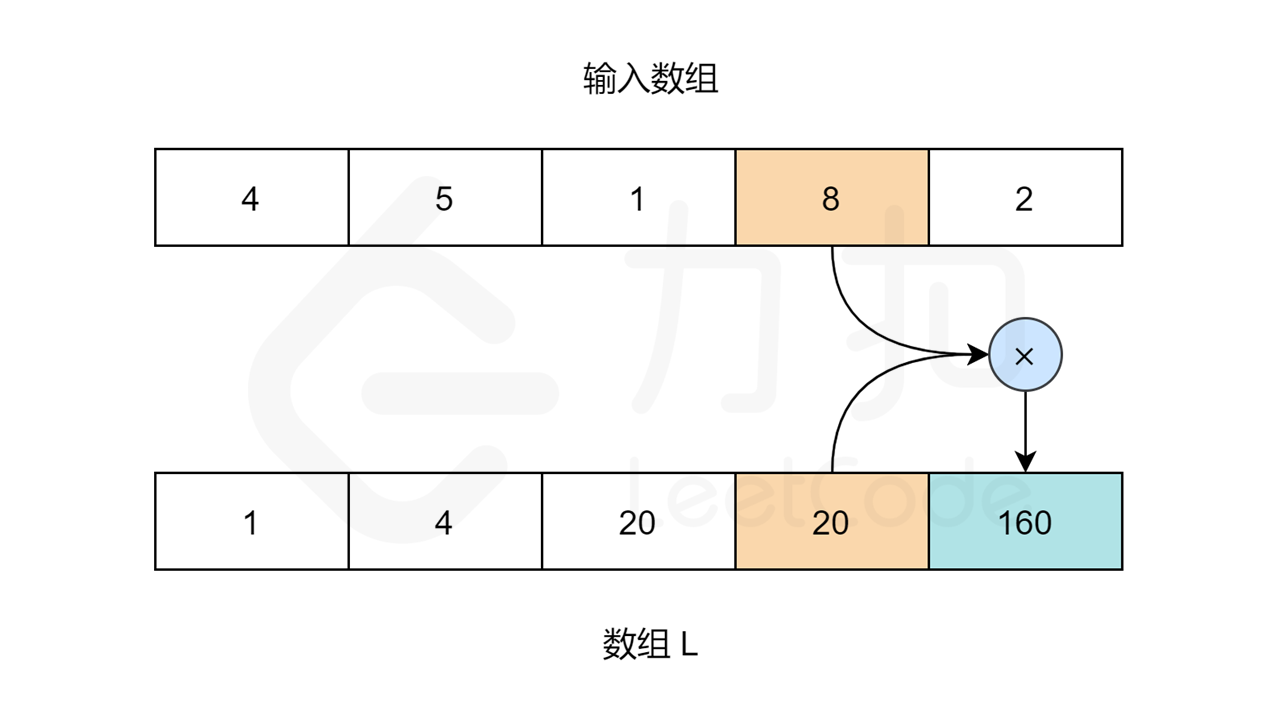
  4. 当 R 和 L 数组填充完成，我们只需要在输入数组上迭代，且索引 i 处的值为：L[i] * R[i] 。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

class ProductExceptSelf {
    public int[] productExceptSelf1(int[] nums) {
        int length = nums.length;

        // L 和 R 分别表示左右两侧的乘积列表
        int[] L = new int[length];
        int[] R = new int[length];

        int[] answer = new int[length];

        // L[i] 为索引 i 左侧所有元素的乘积
        // 对于索引为 '0' 的元素，因为左侧没有元素，所以 L[0] = 1
        // 对于其他元素：L[i] = L[i-1] * nums[i-1]
        L[0] = 1;
        for (int i = 1; i < length; i++) {
            L[i] = nums[i - 1] * L[i - 1];
        }

        // R[i] 为索引 i 右侧所有元素的乘积
        // 对于索引为 'length-1' 的元素，因为右侧没有元素，所以 R[length-1] = 1
        // 其他元素：R[i] = R[i+1] * nums[i+1]
        R[length - 1] = 1;
        for (int i = length - 2; i >= 0; i--) {
            R[i] = nums[i + 1] * R[i + 1];
        }

        // 对于索引 i，除 nums[i] 之外其余各元素的乘积就是左侧所有元素的乘积乘以右侧所有元素的乘积
        for (int i = 0; i < length; i++) {
            answer[i] = L[i] * R[i];
        }

        return answer;
    }
}
复杂度分析
  • 时间复杂度： O(N) , 其中 N 指的是数组 nums 的大小。预处理 L 和 R 数组以及最后的遍历计算都是 *O(N)*的时间复杂度。
  • 空间复杂度： O(N) , 其中 N 值得之数组 nums 的大小。使用了 L 和 R 数组去构造答案， L 和 R 数组的长度为数组 nums 的大小。

方法二：空间复杂度 O(1) 的方法

思路

对于进阶所提到的在常数空间复杂度内完成题目，可以直接将答案存储在输出数组中。先把输出数组当作 L 数组来计算，然后再动态构造 R 数组得到结果。

算法
  1. 初始化 answer 数组，对于给定索引 i , answer[i] 代表的是 i 左侧所有数字的乘积。
  2. 构造方式与之前相同，只是我们试图节省空间，先把 answer 作为方法一的 L 数组。
  3. 之后通过遍历动态构造 R 数组。更新数组 answer[i] = answer[i] * R 。然后 *R = R answer[i] ,其中变量 R 表示的就是索引右侧数字的乘积。
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

public int[] productExceptSelf(int[] nums) {
        int length = nums.length;
        int[] answer = new int[length];

        // answer[i] 表示索引 i 左侧所有元素的乘积
        // 因为索引为 '0' 的元素左侧没有元素， 所以 answer[0] = 1
        answer[0] = 1;
        for (int i = 1; i < length; i++) {
            answer[i] = nums[i - 1] * answer[i - 1];
        }

        // R 为右侧所有元素的乘积
        // 刚开始右边没有元素，所以 R = 1
        int R = 1;
        for (int i = length - 1; i >= 0; i--) {
            // 对于索引 i，左边的乘积为 answer[i]，右边的乘积为 R
            answer[i] = answer[i] * R;
            // R 需要包含右边所有的乘积，所以计算下一个结果时需要将当前值乘到 R 上
            R *= nums[i];
        }
        return answer;
    }
复杂度分析
  • 时间复杂度： O(N) ，其中 N 指的是数组 nums 的大小。
  • 空间复杂度： O(1) ，输出数组不算进空间复杂度中，因此我们只需要常数的空间存放变量。